Ich mochte den Geometrie-Unterricht. Wie war das bei Ihnen? Bei uns wurde noch ganz viel mit dem Geodreieck in ein Koordinatenkreuz gezeichnet, und die gezeichneten Ergebnisse sollten natürlich mit den danach mathematisch ermittelten übereinstimmen. Flächenermittlung, Satz des Pythagoras, Ähnlichkeitssätze, Strahlensätze … alles Konzepte, die im “realen Leben” immer mal wieder anwendbar sind – zum Beispiel beim Patchwork! Von wegen, Mathematik sei nutzlos …
Heute möchte ich erklären, wie Sie die unterschiedlichen Zuschnittmaße berechnen können, wenn Sie in einem Patchworkmuster einfache Quadrate, zusammengesetzte Quadrate und Quadrate aus Dreiecken kombinieren. Denn schließlich sollen die Einzelteile ja aneinander passen und einfach zusammenzunähen sein. Insbesondere die Dreiecke sind da nicht ganz intuitiv. Man kann diese natürlich auf ein Blatt Papier aufzeichnen und abmessen (oder die Maße einer fertigen Vorlage verwenden). Eleganter und viel breiter anwendbar ist aber eine Formel.
Unsere Basisgröße sei eine fertige Kantenlänge von 30 mm (wie in meinen herzigen Miniquilts), die Nahtzugabe sei durchgehend 6,5 mm (= 1/4 inch, somit geeignet für die Patchworkfüßchen #37 oder #57).
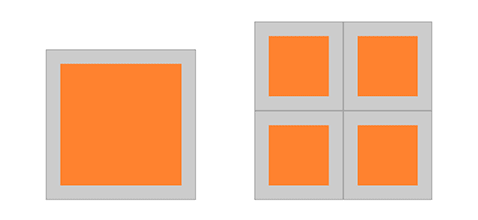
Die Kantenlänge eines Quadrats berechnet sich aus:
Gesamtkantenlänge = Fertige Kantenlänge + 2 x Nahtzugabe
Das ergibt für ein “normales” Quadrat:
Kantenlänge = 30 mm + 2 x 6,5 mm = 43 mm
Ein großes Quadrat soll so groß sein wie ein aus 4 normalen Quadraten zusammengesetztes, also eine fertige Kantenlänge von 2 mal 30 mm haben. Die Ausgangsgröße ist dann:
Kantenlänge = 60 mm + 2 x 6,5 mm = 73 mm
So weit, so einfach. Jetzt wird es spannend: wie berechnet man die Ausgangsgröße, wenn das Quadrat aus 2 Dreiecken bestehen soll?
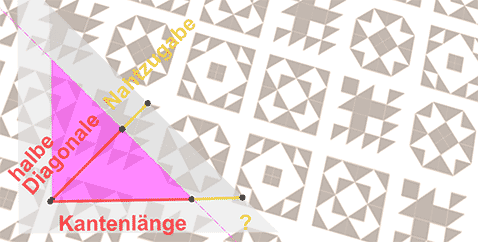
Gehen wir wieder von einem Quadrat mit 30 mm Kantenlänge plus 2 mal 6,5 mm Nahtzugaben aus. Das schneiden wir gedanklich diagonal durch.

An der diagonalen Seite wird die Nahtzugabe, wie an den geraden Kanten auch, parallel zur Kante “angezeichnet”. Nun wollen wir wissen, wie sich das auf die gerade Kante auswirkt, also wie viel länger die Außenkante werden muss.
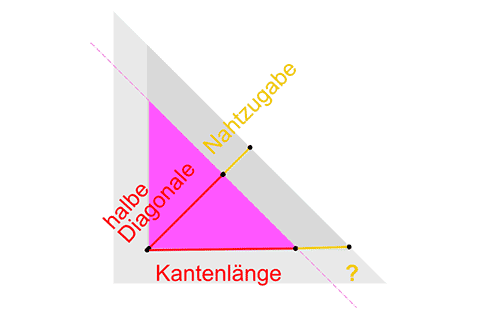
Dabei hilft uns einer der Strahlensätze:
Halbe Diagonale / Nahtzugabe = Kantenlänge / ?
Das ergibt aufgelöst nach ? :
? = Kantenlänge x Nahtzugabe / Halbe Diagonale
Die Diagonale ergibt sich gemäß dem Satz des Pythagoras:
Diagonale = Wurzel aus (Kantenlänge2 + Kantenlänge2)
Demnach heißt die Formel:
? = 2 x (Kantenlänge x Nahtzugabe) / Wurzel aus (Kantenlänge2 + Kantenlänge2)
Wir setzen unsere Maße ein und rechnen:
? = 2 x (30 mm x 6,5 mm) / Wurzel aus ( (30 mm)2 + (30 mm)2 ) = ( 2 x 195 / Wurzel aus (900 + 900) ) mm
= ( 390 / 42,43 ) mm = 9,19 mm
Unser Ausgangsquadrat für die Dreiecke muss also
Kantenlänge = 30 mm + 2 x 6,5 mm + 9,2 mm = 52,2 mm
haben. Die 0,2 mm werden Sie natürlich nicht anmessen 😉 – runden Sie einfach auf 53 mm auf. Man kann sich ohnehin streiten, wie sinnvoll so ein krummes Maß ist, oder ob man nicht besser 55 mm zuschneidet und später ein Itzelbitzelchen mehr zum Begradigen hat. Das können Sie je nach verwendeten Stoffen entscheiden, hier wollte ich Ihnen einfach nur die Berechnung vorführen.
Diese Formel können Sie nämlich immer anwenden, ganz gleich, wie groß Ihre Ausgangsquadrate und Ihre Nahtzugaben werden sollen!
Die Grafiken sind übrigens mit Inkscape gemacht, einem frei zum Download verfügbaren Programm, das sich auch ganz wunderbar zum Entwerfen von Quiltlayouts aus einfachen Grundformen eignet.

Wenn Sie mögen, gebe ich Ihnen demnächst gerne eine Einführung in die Funktionen, die man dafür braucht.
Viel Spaß beim Rechnen!
UPDATE:
Für alle, die nicht gerne Wurzeln berechnen, gibt es einen kleinen Trick: Die Diagonale eines Quadrats von 1 mal 1 ist Wurzel aus 2, also näherungsweise 1,414, die halbe Diagonale dementsprechend 0,707. Das kann man sich zunutze machen und die Formel folgendermaßen umschreiben:
? = (Kantenlänge x Nahtzugabe) / (1/2 x Wurzel aus 2) x Kantenlänge
oder vereinfacht:
? = (Kantenlänge x Nahtzugabe) / ( 0,707 x Kantenlänge )
Das ergibt mit unseren Zahlen:
? = ( 30 mm x 6,5 mm ) / ( 0,707 x 30 mm ) = 195 / 21,21 mm = 9,19 mm
Es gibt glücklicherweise meistens mehr als einen Weg zum Glück …
 BERNINA Corporate Blog –
BERNINA Corporate Blog –




Bin nach einer schlaflosen Nacht(nicht deswegen) und der Übung im dunkeln und im Kopf die Kantenlänge eines in zwei Dreiecke zu teilenden Quadrates zu ermitteln nur mithilfe des Pythagoras auf das gleiche Ergebnis gekommen. Für Strahlensatz war da kein Speicher mehr. Da war ich froh hier eine passende Mathestunde zu finden. Braucht man die Kantenlänge zur Berechnung der gelben Linie in obiger Skizze denn? Hängt die zu erfahrene Länge nicht ausschließlich von der Länge der Nahtzugabe ab? Oder hab ich einfach nur (Anfänger-)Glück gehabt? Liebe Grüße, Gesine
Hallo Martina!
Wie groß soll deine Nahtzugabe sein?
Du sagst deine Zuschnitte sind 22,5 cm. d.h. bei 20 cm fertiger Länge hast du 1.25 cm (x 2) Nahtzugabe. Bei 0,7 cm Nahtzugabe solltest du 21,4 cm nehmen.
Ich rechne sonst immer mit inch. Polster 40 x 40 cm = 16 x 16 Inch. Für ein Top mit 4 gleichen Quadraten schneide ich:16/2 = 8 Inch plus 2 x Nahtzugabe von 1/4 Inch = 81/2 Inch Kantenlänge für das Zuschnittquadrat.
Liebe Grüße
Hedwig
Hallo! Ich möchte ein Patchworkkissen 40 x 40 nähen, bei dem die Vorderseite aus 4 Quadraten besteht. Wie groß muss das Schnittmuster eines Quadrats sein? Ich habe 22,5 cm genommen. Stimmt das? Vielen Dank für Eure Hilfe, Martina
Kleiner Tipp:
Es gibt Quadratraster und Dreieckraster von Freudenberg – daraus kann man alle Schablonen super herstellen ohne rechnen zu müssen.
Erst das Muster einzeichnen, dann die einzelnen Teile mit Nahtzugaben ausschneiden. Mache ich mit Schülern so – denn Mathematik in der Hauptschule ist nicht sehr angesagt.
Wer keinen PC hat kann aber auch Wurzel ziehen mit dem guten alten Rechenschieber!!!
Es ist toll wie vielfältig dasQuilten ist, es braucht “Kopf-Hand und Herz(Auge)” .
Noch einen schönen Sonntag
wünscht euch eine Anfängerin
Christel
vielen Dank für die Prompte Antwort. Nun werde ich mir leichter tun.
Danke
Gertrud
Ohhhhh, was bin ich sooo froh, daß ich eine “Freischneiderin” bin:-))). Aber trotzdem eine glatte “1” ins Klassenbuch für Ursula!!
Hallo Gertrud,
von Hand kann ich das auch nicht ;-).
Die Quadratwurzel kannst Du aber leicht auf jedem Taschenrechner finden oder, wenn Dir das vertrauter ist, in Excel oder OpenCalc.
Ein Tipp: Die (Quadrat)-Wurzel ist ja die dem Quadrieren “entgegengesetzte” Rechenoperation. Wenn Du Dir nicht sicher bist, ob Du die richtige Funktion erwischt hast, mach also einfach die Probe mit einer bekannten Rechnung, z.B.: 4 mal 4 = 16. Also gib Wurzel von 16 ein, und wenn 4 rauskommt, passt es.
Ich habe den Artikel übrigens gerade um einen alternativen Rechenweg ergänzt – jetzt ist Wurzelziehen nicht mehr nötig.
Viele Grüße
Ursula
hallo Ursula
auf die Gefahr hin das ich mich fürchterlich blamiere. Ich weiss leider nicht mehr wie man eine Wurzel ausrechnet. Also wie komme ich von (900+900) auf 42,43
gruss Gertrud
Vielen Dank für die super Lektion, Ursula! Also, wenn jetzt zu mir in der Schule jemand sagt: ‘Ich möchte später einmal mit Textilien arbeiten. Welche Fächer sind da nützlich?’, dann werde ich sofort sagen: ‘Mathematik!’
Lorchen